Periodic Orbits Around L₁

In the cislunar relative motion frame of reference, several aesthetic patterns emerge when a spacecraft has certain initial positions and velocities. These patterns can be optimized to create periodic orbits where spacecraft can appear to have an orbit in the cislunar relative motion frame. The periodic orbits discussed on this site are the Lyapunov, northern and southern halo, northern and southern axial, vertical, butterfly, and prograde orbits. In this section, the periodic orbits of Lagrange point L₁ are shown, where L₁ is the point in between the two bodies of mass but closer to the secondary body.

Lyapunov

A Lyapunov orbit is a planar orbit about either L₁, L₂, or L₃ in the radial and in-track plane. These orbits revolve around the respective Lagrange point in the clockwise direction when viewing the positive cross-track direction.

Due to the simple geometry of the Lyapunov periodic orbit, these periodic orbits can be solved with the two-dimensional state transition matrix (STM). Since the Lyapunov orbits are planar, only the x and y axis components need to be considered in the STM as shown on the STM page. The key points of interest when solving for the Lyapunov orbits is that the radial velocity is 0 when crossing the radial axis.

Multiple Lyapunov periodic orbits can be plotted together to show the full form of the Lyapunov orbit about L₁ as shown in Figure 5-1. From the compiled plot, a conclusion drawn is that the Lyapunov orbit has a maximum size where the rings begin at L₁ and grow in size until the periodic orbits intersect the Moon.

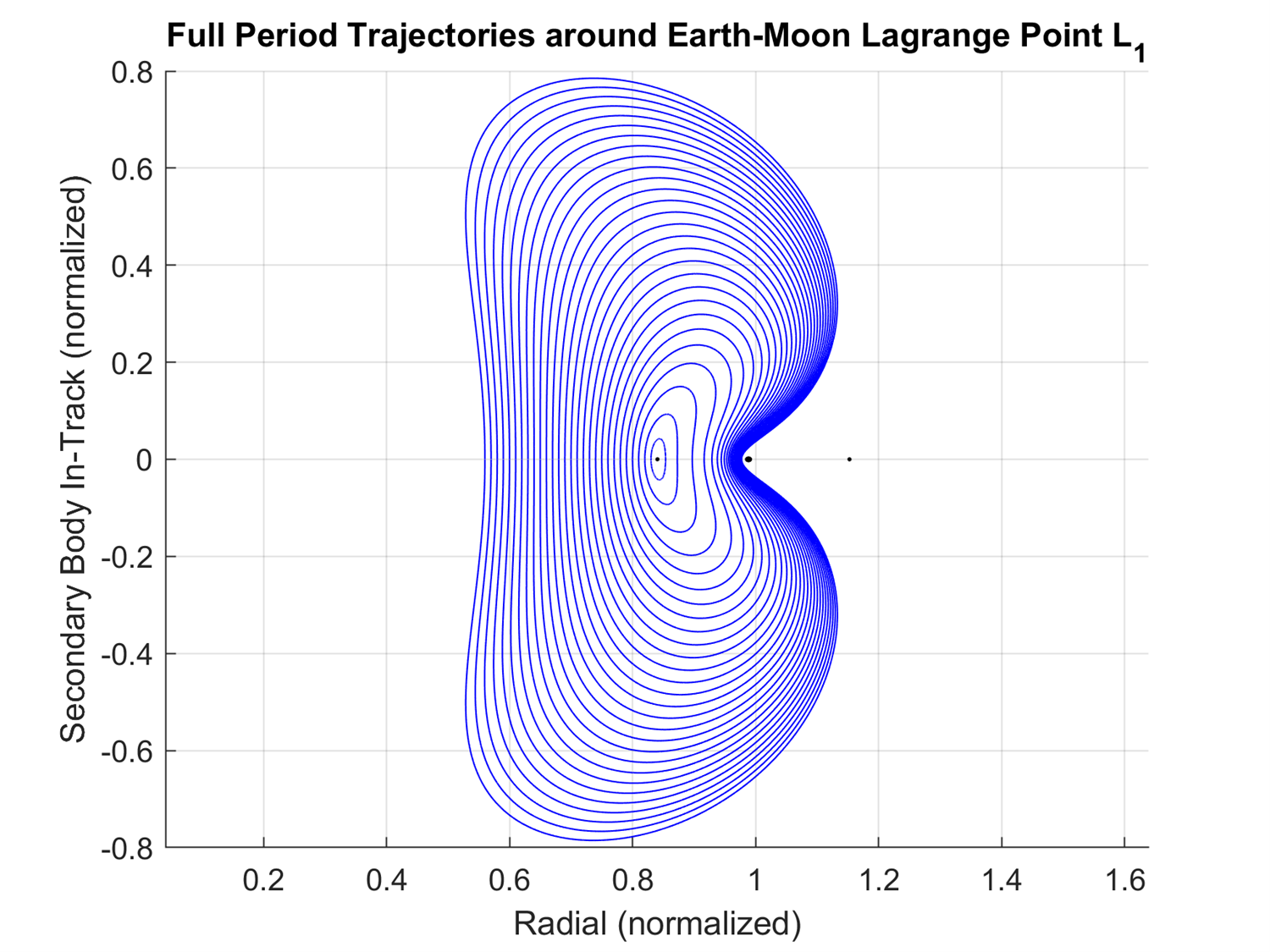
Figure 5-1: The Lyapunov periodic orbits around L₁.

Northern Halo

Lagrange points L₁ and L₂ each have a set of northern and southern halo orbits. A simplified way to determine whether a halo orbit is northern or southern is whichever side of the radial and in-track plane the orbit spends the majority of its time in is the type of halo orbit.

The geometry of the halo orbits is more complex than the Lyapunov orbits in that they are three-dimensional and require the three-dimensional STM from the STM page. The key points of interest in its orbit are its periapsis and apoapsis, or the smallest and largest radial (or cross-track) positions. At the periapsis, the radial and cross-track velocities are 0, and similarly at the apoapsis, the radial and cross-track velocities are 0. This allows the three-dimensional STM from the STM page to be used to solve for both Lyapunov and halo orbits.

Figure 5-2 shows the compilation of the northern halo periodic orbits with L₁, L₂, and the Moon labeled. Figure 5-3 shows the same compilation of the northern halo orbits about L₁ but from the positive radial direction looking towards the center of the frame. Figure 5-4 shows the same compilation of the northern halo orbits about L₁ but from the negative in-track direction looking towards the Moon.

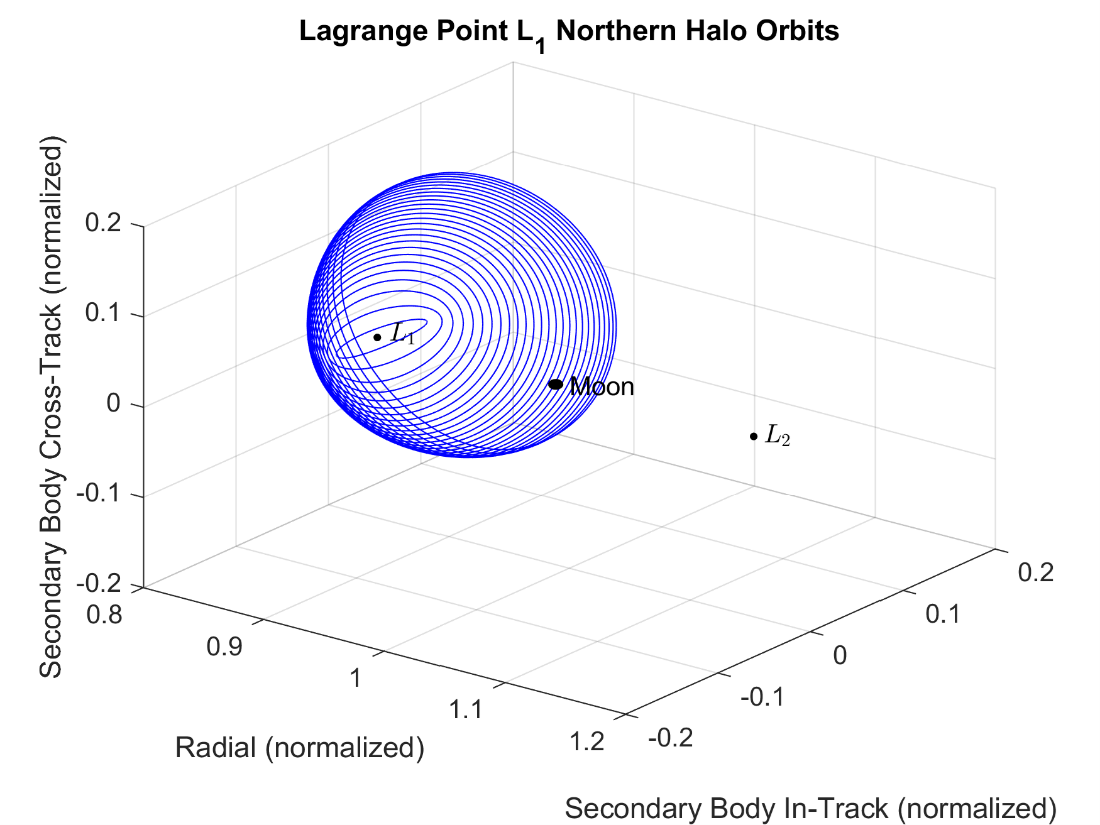
Figure 5-2: The northern halo periodic orbits about L₁.

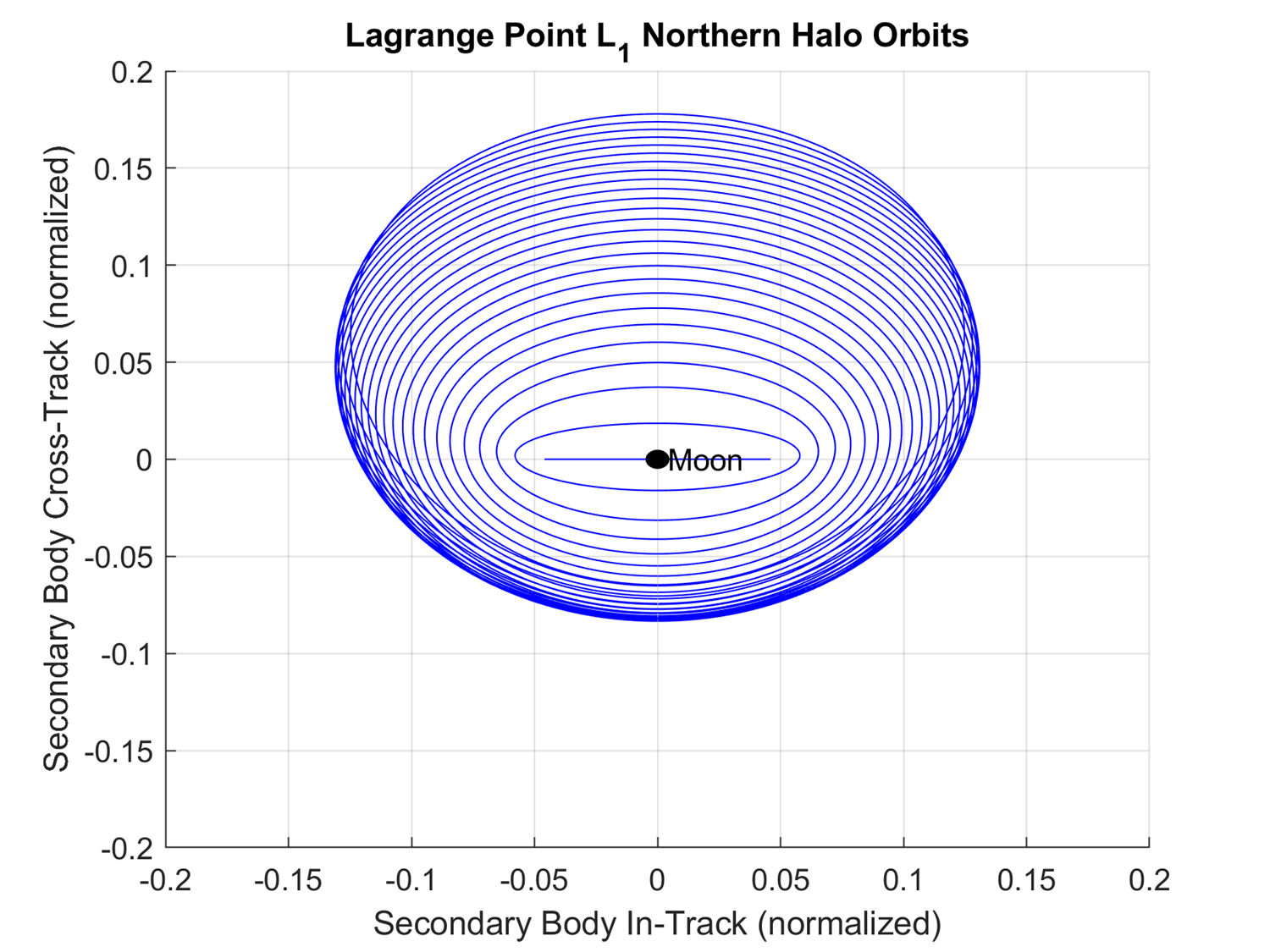
Figure 5-3: The northern halo periodic orbits about L₁.

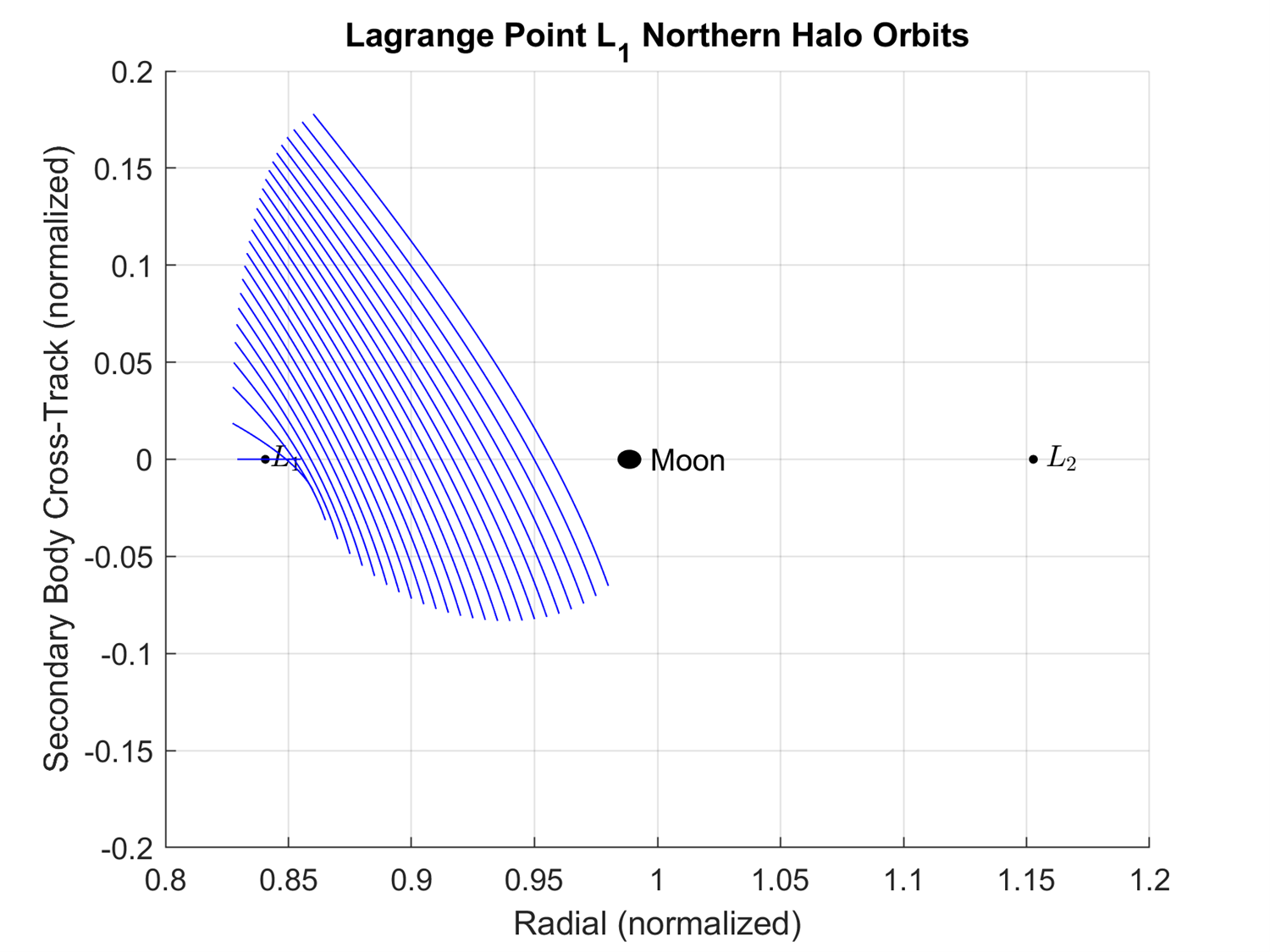
Figure 5-4: The northern halo periodic orbits about L₁.

Southern Halo

The southern halo orbits are similar to the northern halo orbits but spend the majority of their orbit below the radial and in-track plane. The method of calculating the southern halo orbits is identical to that of the northern halo orbits shown on the STM page.

Figure 5-5 shows the compilation of the southern halo periodic orbits with the L₁, L₂, and the Moon labeled. Figure 5-6 shows the same compilation of the northern halo orbits about L₁ but from the positive radial direction looking towards the center of the frame. Figure 5-7 shows the same compilation of the northern halo orbits about L₁ but from the negative in-track direction looking towards the Moon.

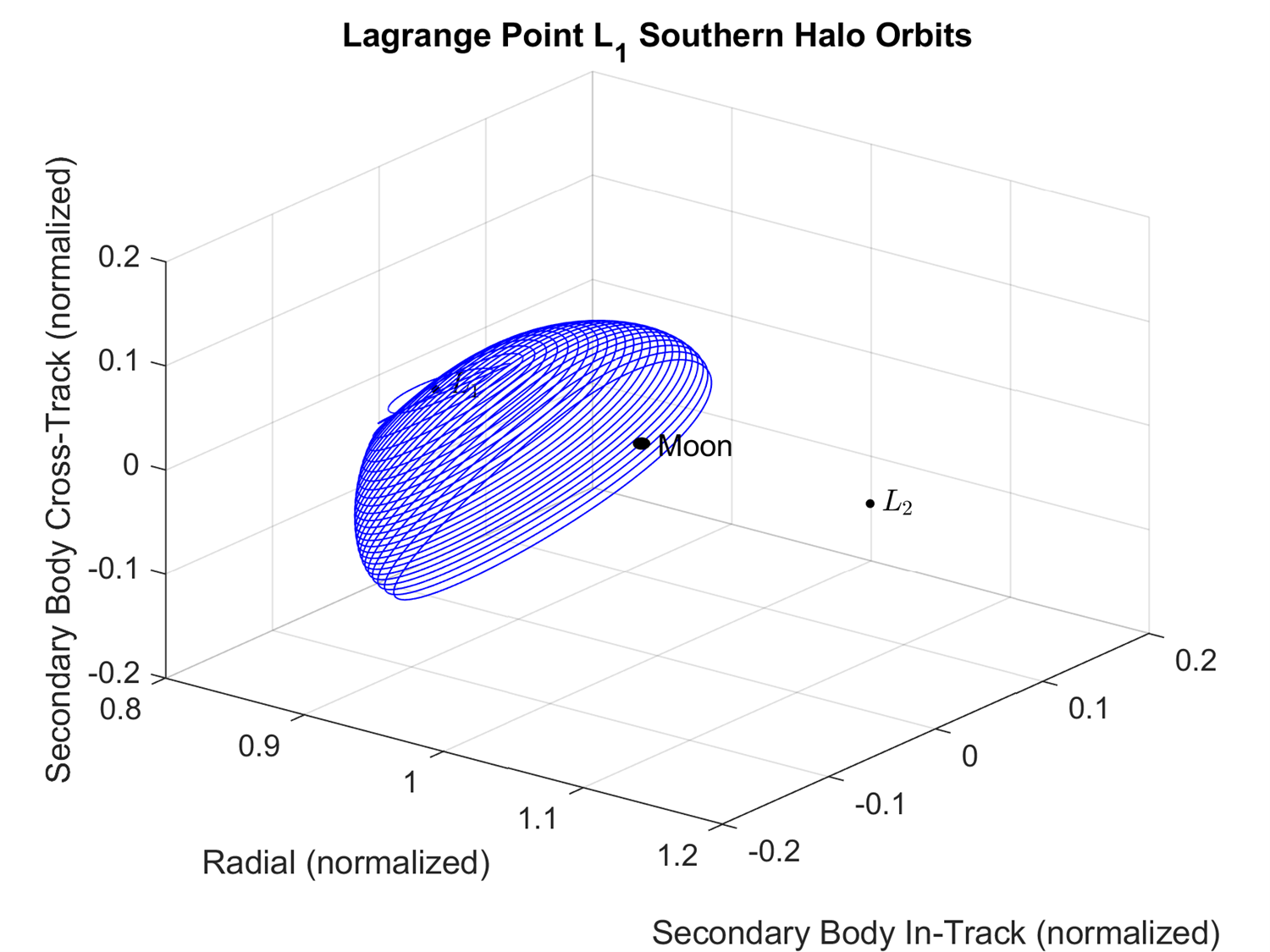
Figure 5-5: The northern halo periodic orbits about L₁.

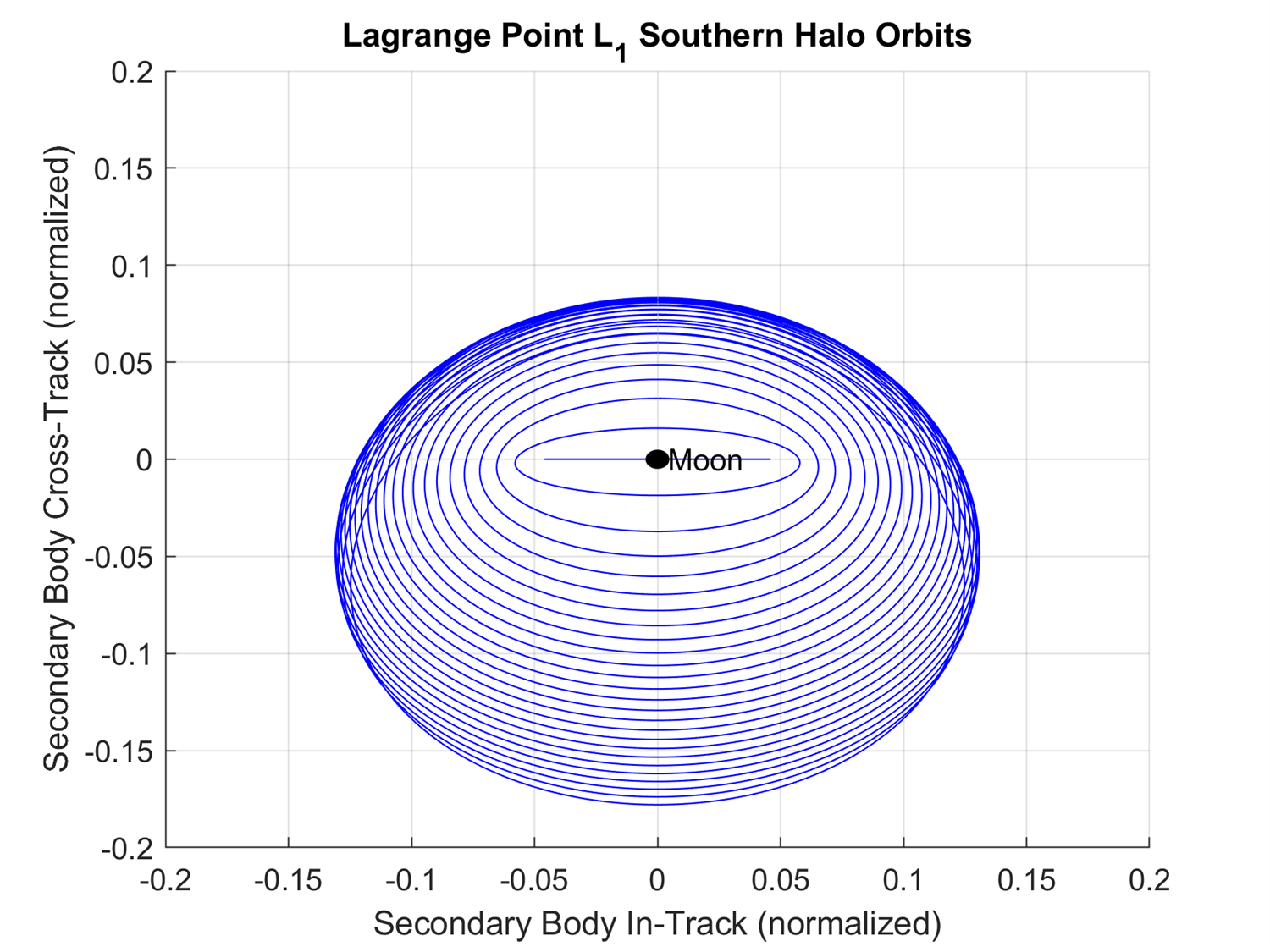
Figure 5-6: The northern halo periodic orbits about L₁.

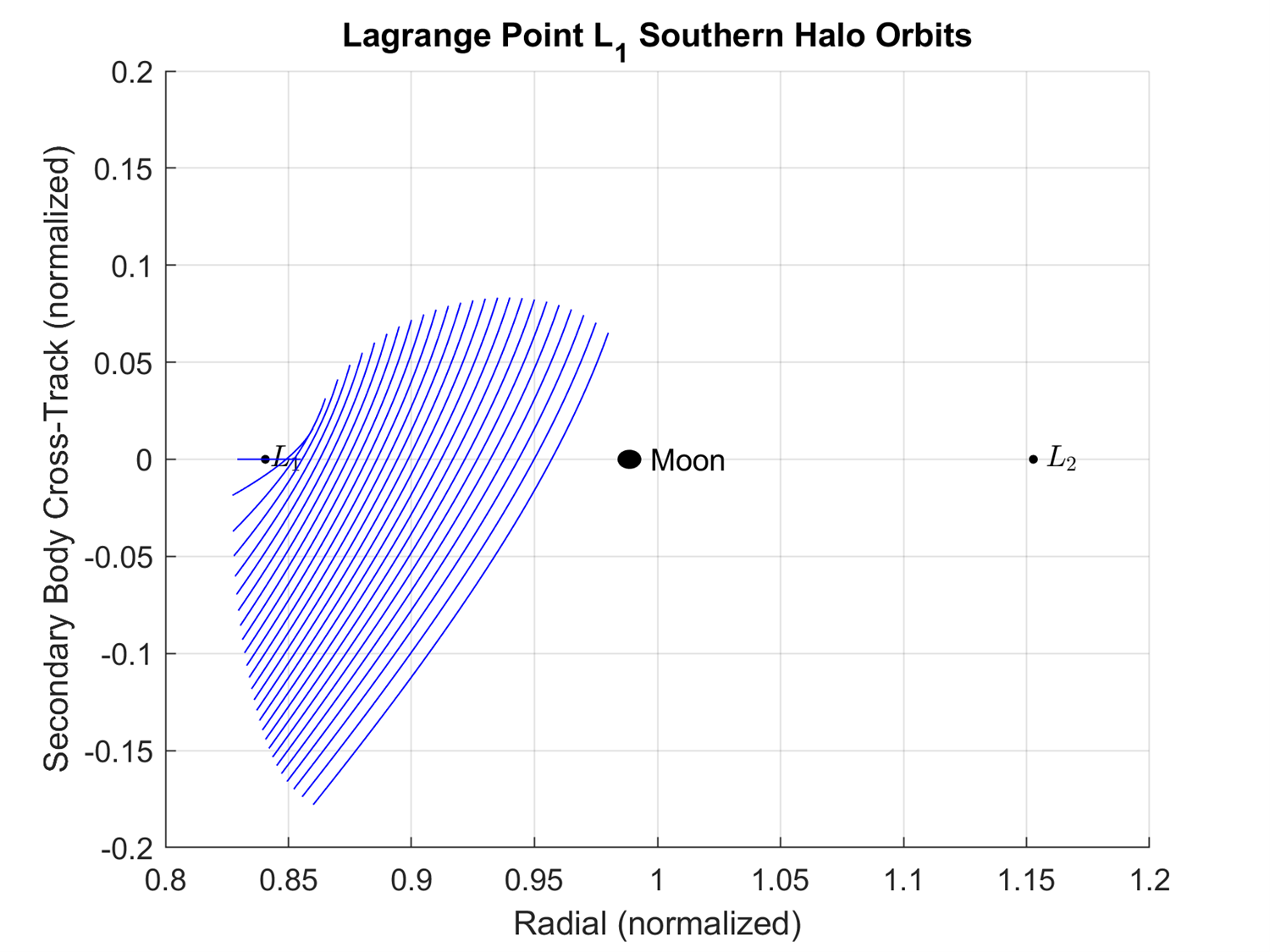
Figure 5-7: The northern halo periodic orbits about L₁.

Vertical

Vertical periodic orbits have a bit more complex orbital geometry than the Lyapunov or halo orbits. The vertical family of periodic orbits form a figure eight intersecting the radial axis, which means at the intersection, its in-track and cross-track positions are both 0. However, there is a non-zero value for both the in-track and cross-track velocities at the intersection. Due to the introduction of a non-zero velocity in the cross-track direction, an adjusted STM needs to be used as shown on the STM page.

Figure 5-8 shows the compilation of the vertical periodic orbits with the L₁, L₂, and the Moon included in the plot.

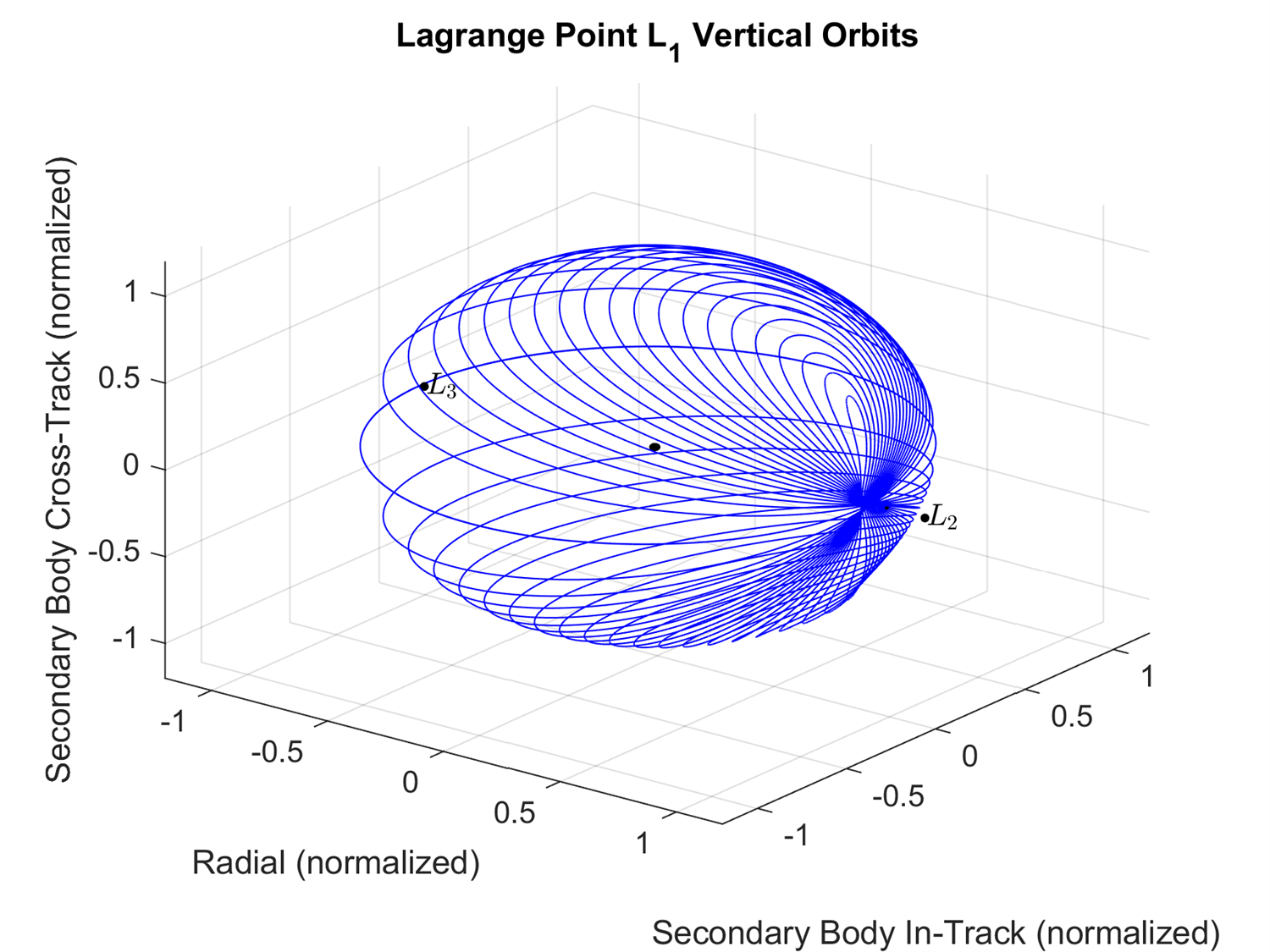
Figure 5-8: The northern halo periodic orbits about L₁.