Cislunar Space

The emphasis of this website is on the natural orbital motion in the space surrounding but within the vicinity of both the Earth and the Moon and how this space can be utilized for navigation. This volume of space is referred to as cislunar space, and although the exact definition of cislunar has varied in previous years to include the Moon's sphere of influence, or the generous volume of spherical space extending out to the furthest end of the Moon's sphere of influence. For this website, the latter will be the definition used.

In such distances from Earth, traditional orbital mechanics do not easily translate, and in fact, near-Earth relative motion orbital mechanics that is commonly understood by the space community do not apply. Not too far past geostationary Earth orbit (GEO), the gravitational force of the Moon must be considered and must not be assumed negligible in quick calculations. At such distances, many orbits no longer follow a clean orbiting pattern as they do within GEO as they are no longer perfectly planar, and their trajectories can vary wildy.

A simple way to view cislunar trajectories in the synodic reference frame, which is derived nearly identically to the relative motion reference frame used for rendezvous and proximity operations (RPO). The RPO frame is used by organizations within the space community such as the National Aeronautics and Space Administration (NASA) for docking spacecraft with the International Space Station (ISS) of for placing spacecraft into position within constellations. The RPO frame consists of the radial, in-track, and cross-track (RIC) direction components. In this frame, the radial direction represents the direction from the Earth through the point of interest as the origin then directly zenith away from Earth, the in-track direction represents the direction from the point of interest into the direction of its flight path angle, and the cross-track direction represents the direction from the point of interest to the direction normal to the radial and in-track directions.

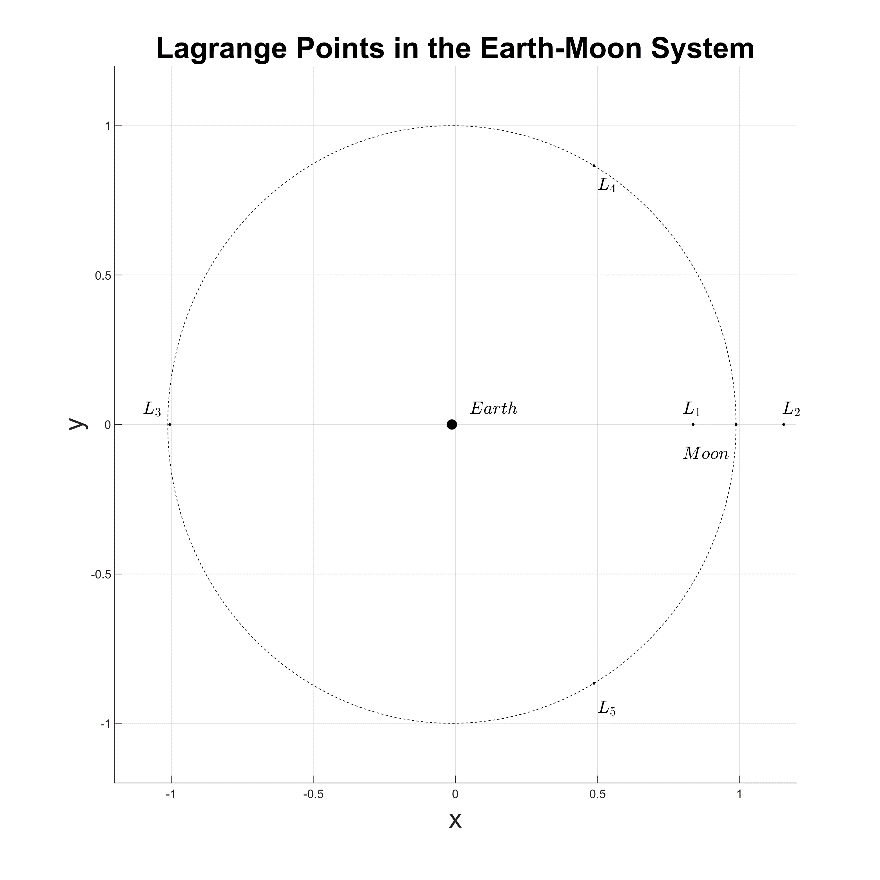
Figure 1-1: The fixed frame and Lagrange points of the Earth-Moon system cislunar relative motion reference frame.

Although the units in this paper are normalized so that the distance between the Earth and Moon equals one, another useful approach is referring to the distances in terms of multiples of GEO. When referring to the distance in terms of multiples of GEO, the Moon resides at an average distance just past 9 GEO. At an average distance of 384,400 km and with GEO being 42,164 km, the Moon is at an average distance of 9.117 GEO. With an average distance from Earth of 384,400 km, the Moon's distance actually varies from about 363,104 km at perigee to 405,696 km at apogee, or 8.612 GEO and 9.622 GEO respectively.

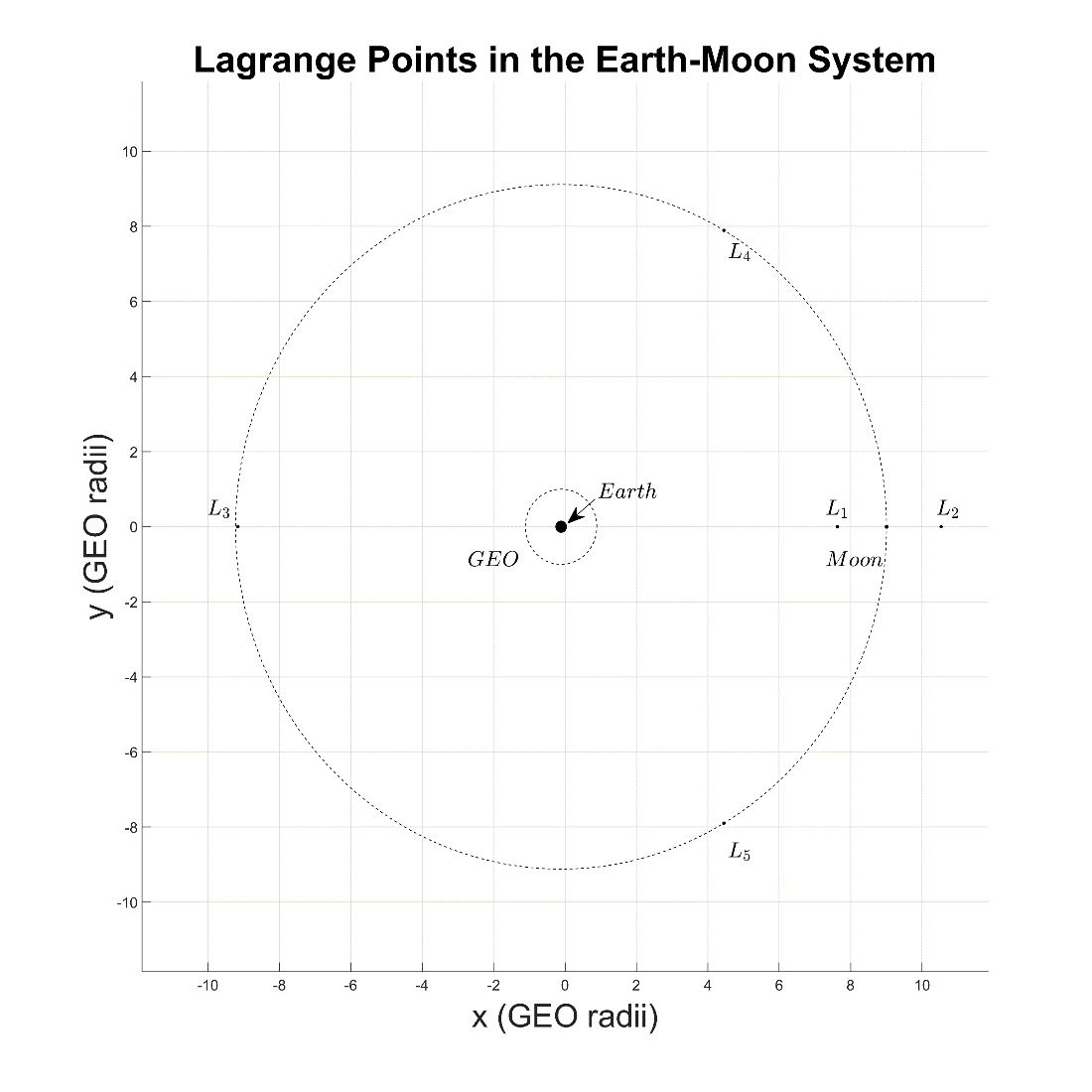
Figure 1-2: The fixed frame and Lagrange points of the Earth-Moon system cislunar relative motion reference frame in terms of GEO radii instead of normalized units.

An alternative proposal to view the cislunar relative motion reference frame is to shift the entire frame to the right so that the Earth is at the center of the reference frame. This allows for an easier understanding of the reference frame by eliminating the need to recall the barycenter being at the center of the reference frame. An example of this is shown in Figure 1-3. However, this figure is just a proposal, and the figures presented in this document follow the convention used in Figure 1-1.

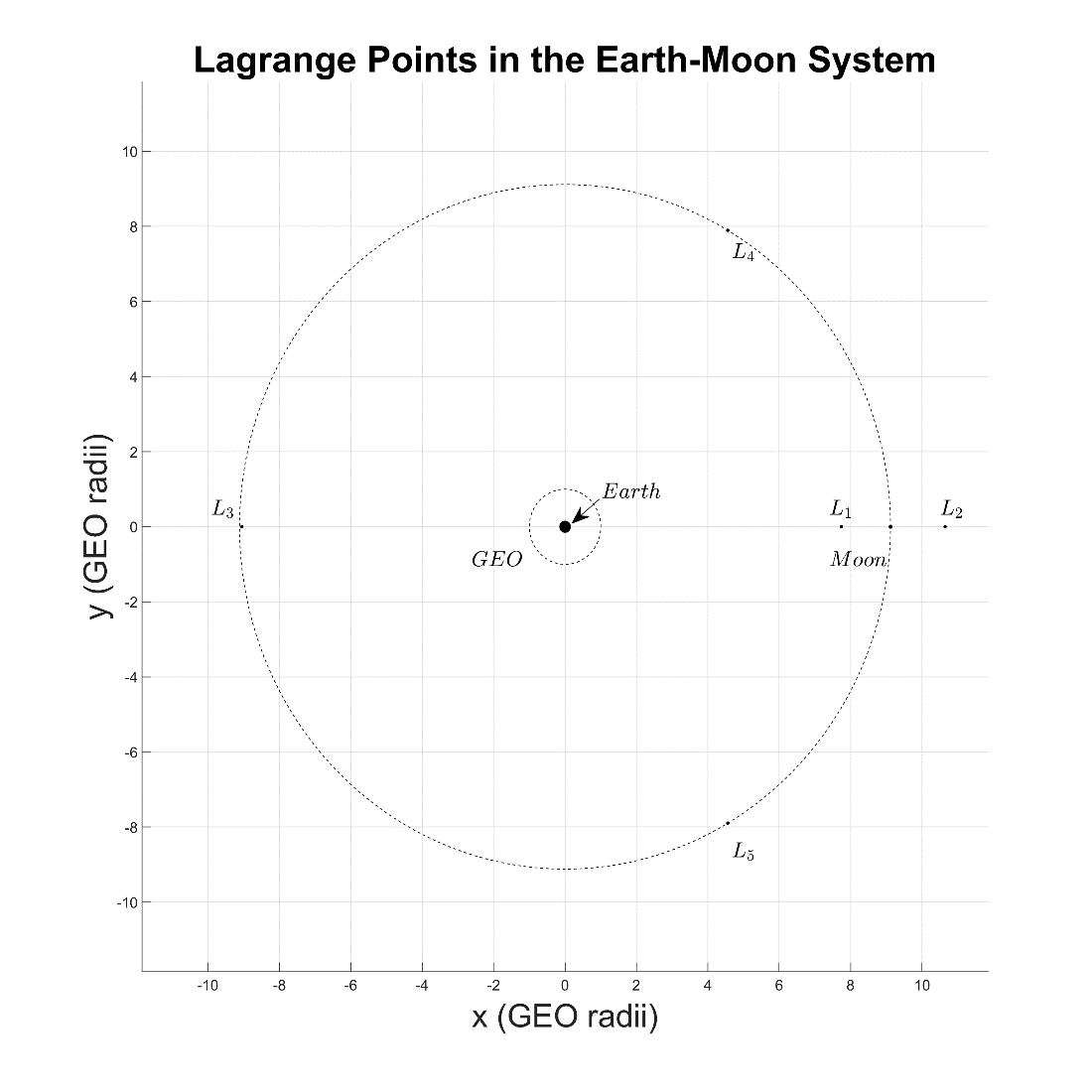
Figure 1-3: The fixed frame and Lagrange points of the Earth-Moon system cislunar relative motion reference frame in terms of GEO radii instead of normalized units with Earth at the center.