Lagrange Points of an Eccentric Three-Body System

When a third body of significant mass is introduced to the eccentric system, there are noticeable effects on the Lagrange points and the Jacobi constant. However, these are only noticeable when the third body is offset in its rotation by 90°. Another characteristic of the addition of a third body is that when the third body's semimajor axis is greater than the second body, the third body drifts in a clockwise direction. When the third body's semimajor axis is less than the second body, it drifts in the counterclockwise direction.

In Figure 5-1, a third body with twice the semimajor axis, half the eccentricity, and half the mass of the Moon is introduced to the Earth-Moon system. When the third body lags 90° behind the Moon, the greatest effect appears on the system where a brief gap in the Jacobi energy field appears. This gaps means that there is a higher Jacobi constant resulting from the gravitational force overcoming the centrifugal force.

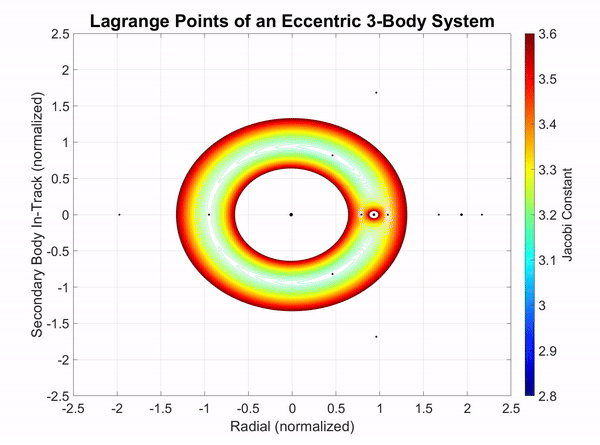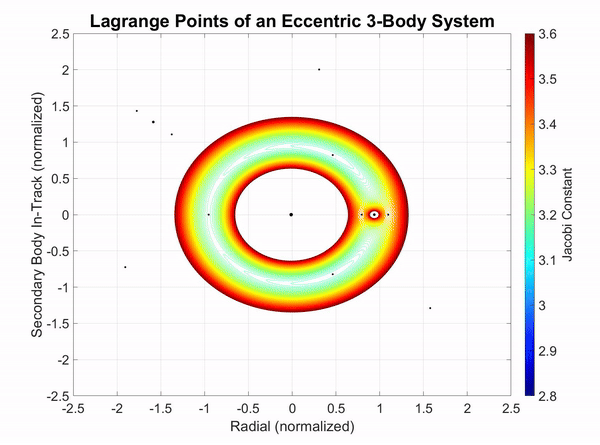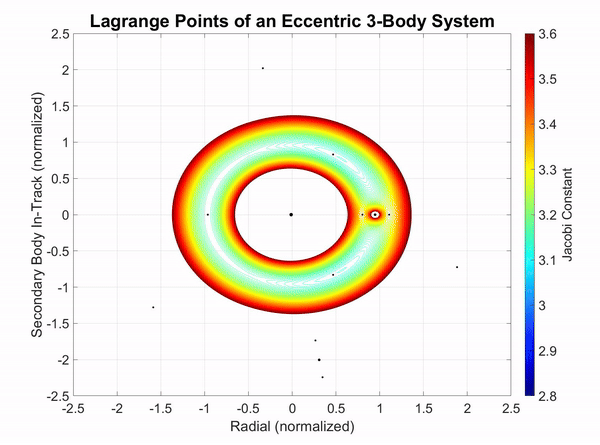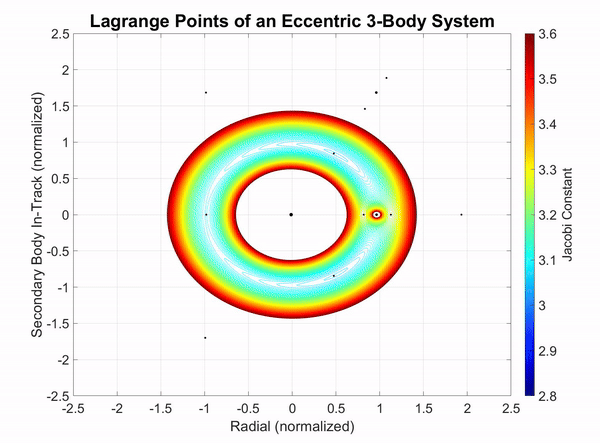
Figure 3-1: The Jacobi constant visualized in an eccentric three-body system.