Lagrange Points of an Eccentric Two-Body System

When analyzing the CR3BP and comparing it to a real two-body system, the obvious difference is that in reality, there are not perfectly circular two-body systems. The most significant two-body systems from the perspective of Earth are the Earth-Moon and Sun-Earth systems. Figure 2-1 shows the Earth-Moon system in the synodic frame, and the Moon's eccentricity becomes apparent as it causes the Lagrange points to ebb and flow. The Yellow lines in the figure indicate the position of the Lagrange points traced out over time. When the Moon is at its perigee, the Lagrange points are at their closest point to Earth and vice versa for when the Moon is at apogee.

The Moon has an eccentricity of 0.1124 where its perigee is 36,000 km and its apogee is 405,000 km. This presents a problem when maneuvering a spacecraft to a Lagrange point that is constantly changing. A spacecraft needs to maneuver to a desired Lagrange point, such as L₁ for example, and alter its eccentricity to match the Moon's. Then, the spacecraft will ebb and flow along with L₁ and the Moon and be able to enter into a halo orbit around the Lagrange point or position itself at the Lagrange point.

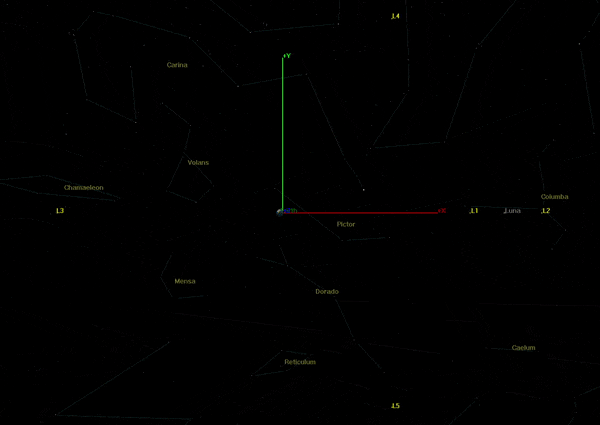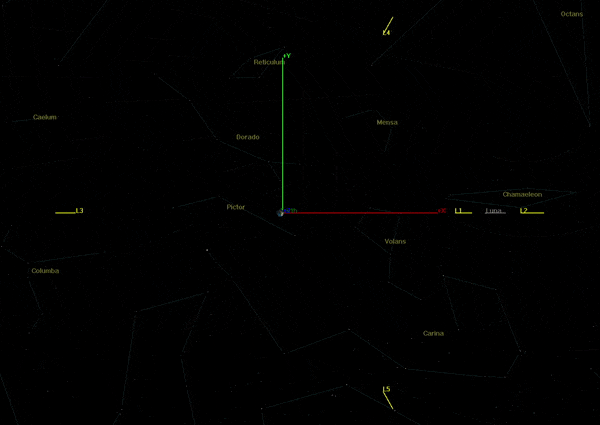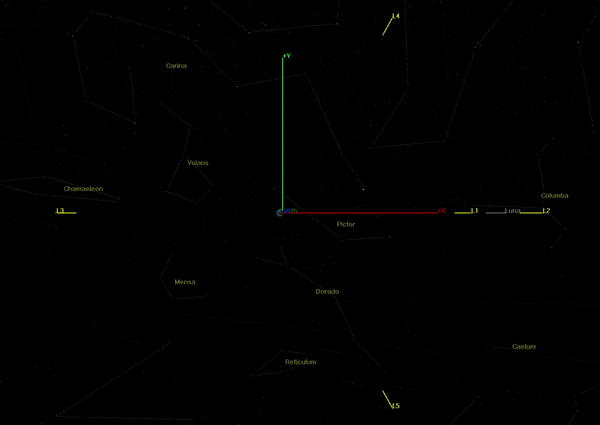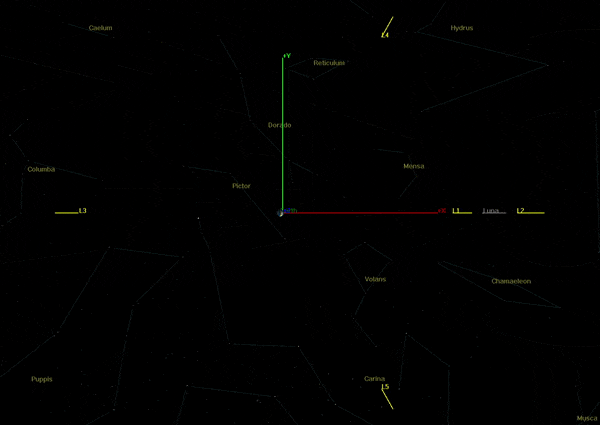
Figure 2-1: The Earth-Moon rotating synodic frame with Moon perigee and apogee of 360,000 km and 405,000 km, respectively.

Figure 2-2 below shows the Earth-Moon rotating synodic system where the rotating frame stays fixed on the Moon as it orbits Earth in an eccentric orbit. The Lagrange points follow the stable valley points of L₄ and L₅, as well as the unstable saddle points of L₁, L₂, and L₃.

From Figure 2-2, it appears that there is a significant energy diffrence between the Moon's perigee and apogee. When the synodic motion is sped up, it appears to ebb and flow where the energy required to traverse through cislunar space past the Moon, L₁, and L₂ is significantly less during perigee. The distance unit in the figure is the semimajor axis of the Moon orbiting the Earth. However, the frame rotates with the Moon, so its centrifugal force follows the Moon. If the rotation of the frame were to follow the mean motion of the Moon about Earth, then the Moon would form a 2 by 1 natural motion circumnavigation (NMC) as shown in Figure 2-3.

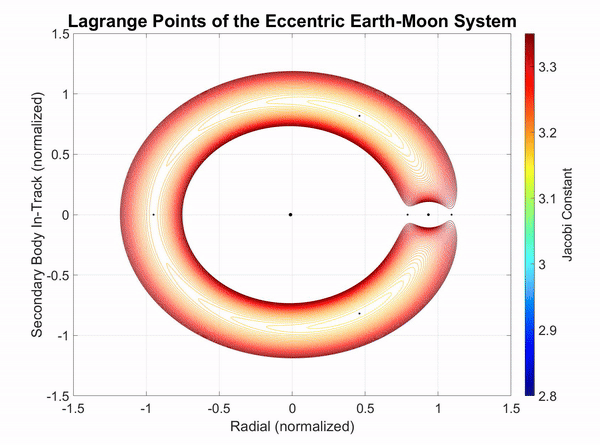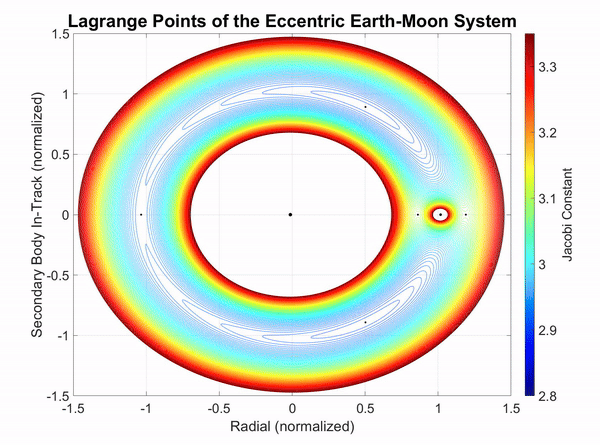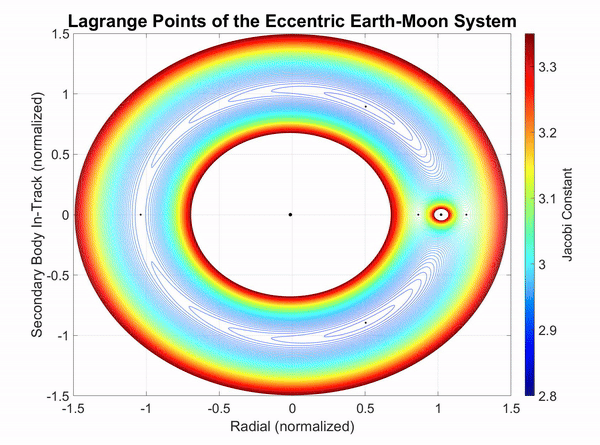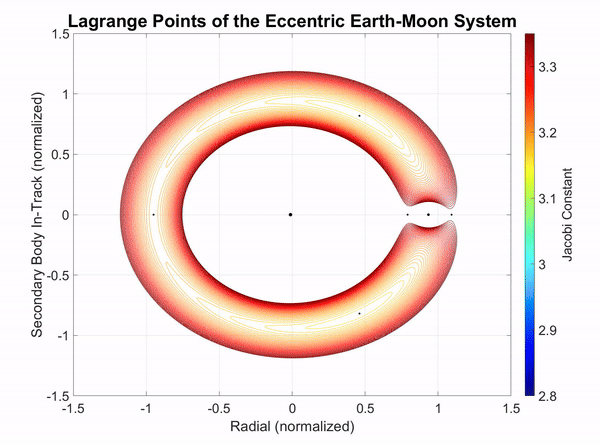
Figure 2-2: The dynamic Lagrange points of the eccentric Earth-Moon system.

Since the Jacobi constant contour ebbs and flows, the two extremes when the Moon is at perigee and apogee can be viewed separately to visualize the difference as shown in Figure 4-3 and Figure 4-4. In these figures, the mean motion of the reference frame is that of the average distance to the Moon of 384,400 km.

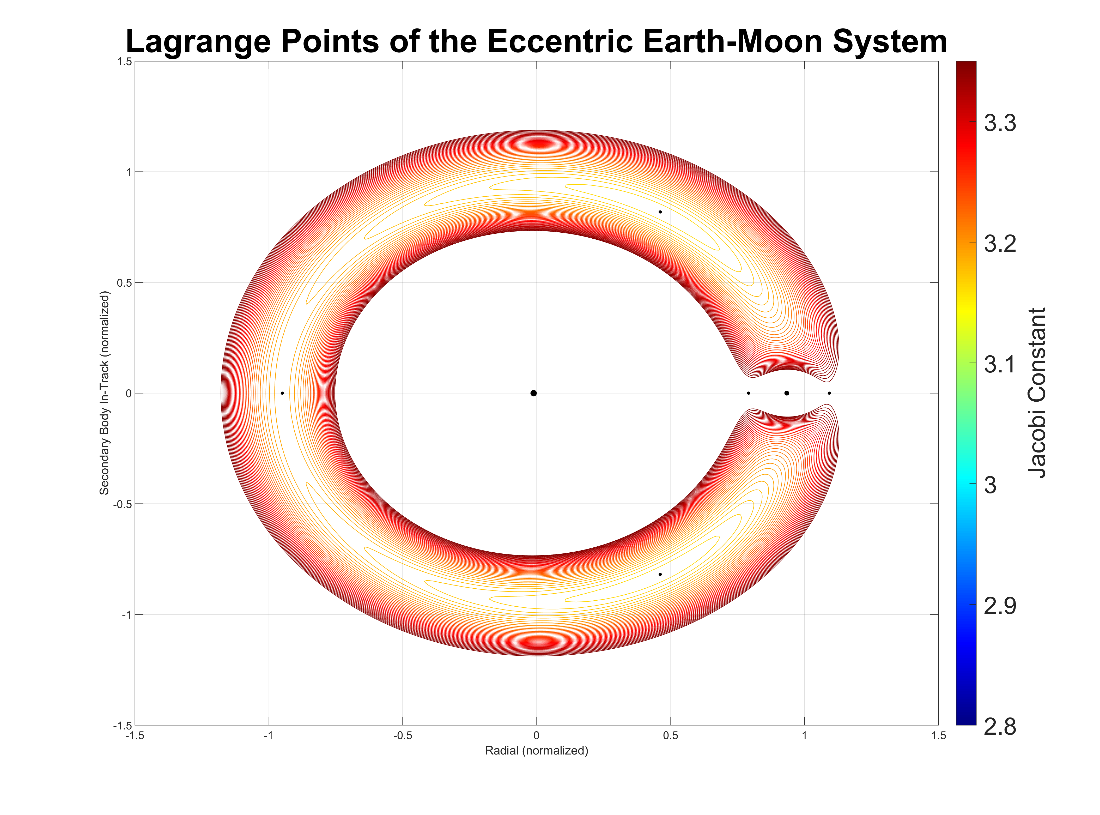
Figure 2-3: Dynamic Jacobi constant of the eccentric Earth-Moon system at Moon perigee.

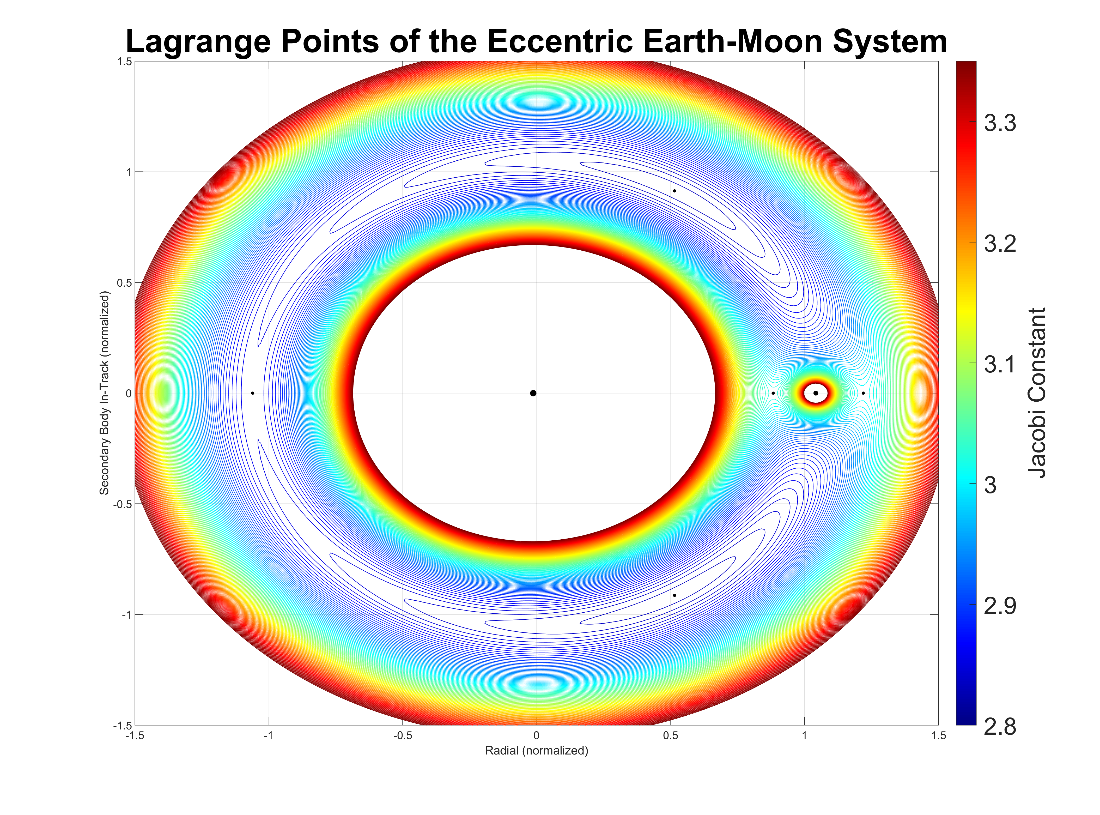
Figure 2-4: Dynamic Jacobi constant of the eccentric Earth-Moon system at Moon apogee.