The Circular Restricted Three-Body Problem

Equations of Motion for the Circular Restricted Three-Body Problem (CR3BP)

Below are the equations of motion for the Circular Restricted Three-Body Problem (CR3BP). These are a form of relative motion where the primary body is near the center of the frame shifted to the left by a value of π₂r₁₂, and the secondary body is in the positive radial direction shifted to the right of the frame by a value of π₁r₁₂. Below shows the equations of motion when the distance between the Earth and the Moon is normalized to a value of 1.

Locations of the Lagrange Points

Within this relative motion system with two bodies of mass, there are five points where the gravitational and centrifugal force balance. At these points, a spacecraft or other body of mass could theoretically be placed and remain at the point indefinitely. These five points are called Lagrange points. There are three Lagrange points along the radial axis and two Lagrange points at a 60° angle to both the primary and secondary bodies of mass. The Lagrange points in the Earth-Moon system are shown in Figure 1-1 below.

The first three Lagrange points are found by solving for x in the equation below. Note that the equation below solves for their x component on the axis of the two bodies. The y components for the first three Lagrange points are all 0 since they all lie on the axis of the two bodies.

The following figures show the Lagrange points for the Sun-Earth, Earth-Moon, and Saturn-Titan two-body systems.

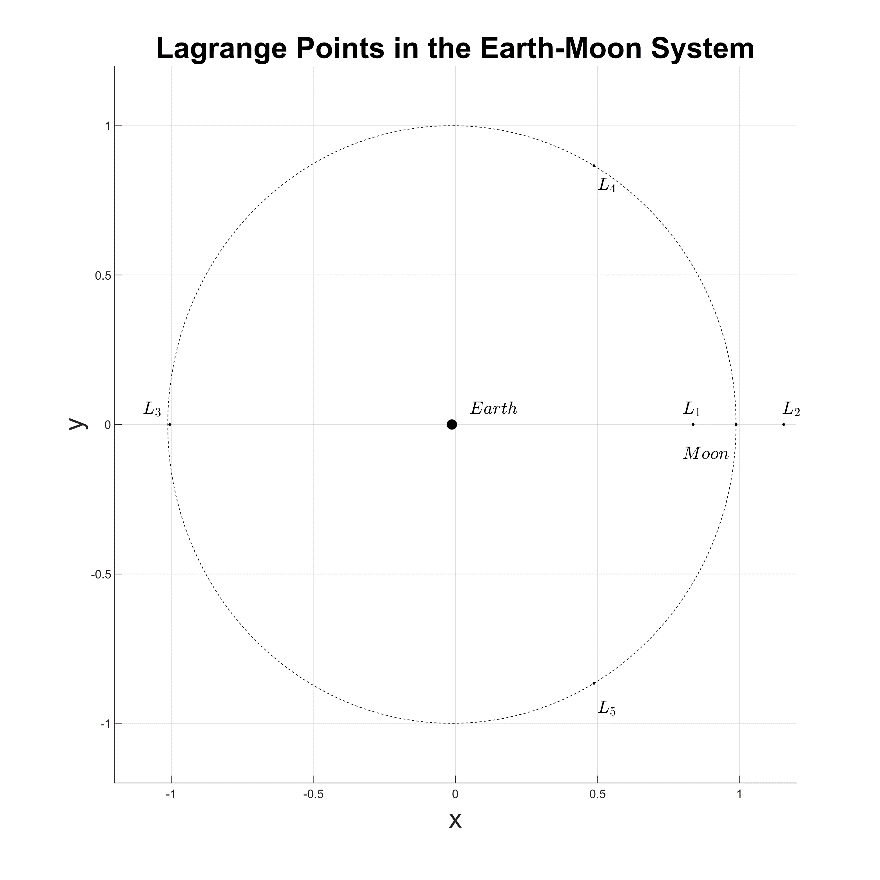
Figure 1-1: The Lagrange points of the Earth-Moon system.

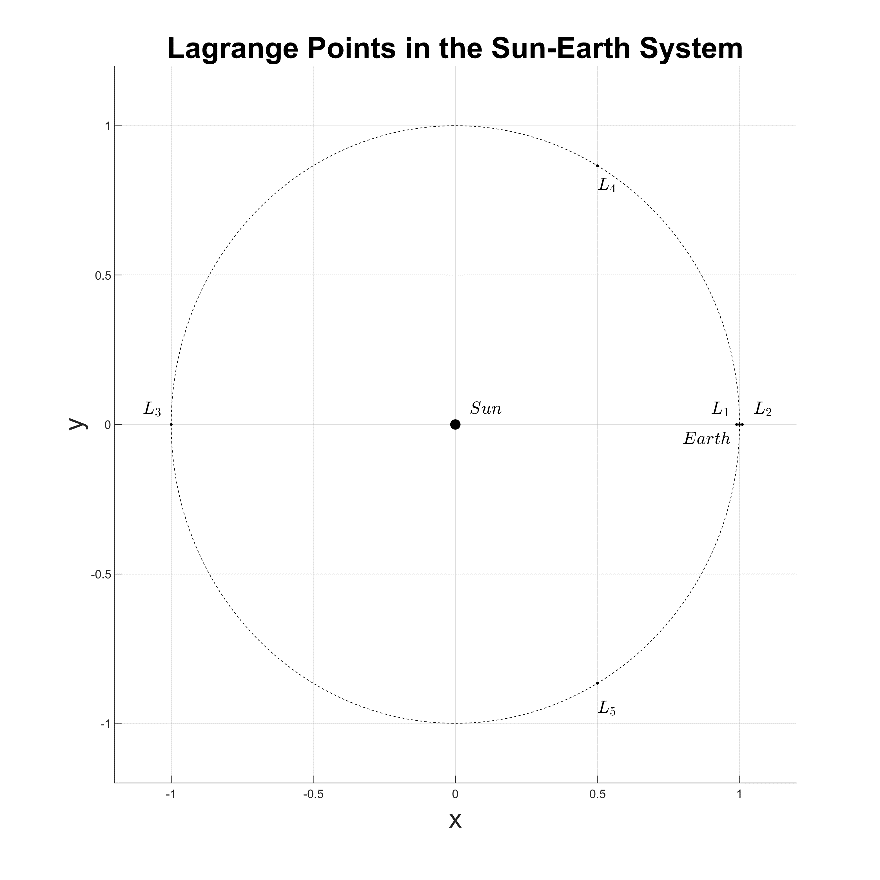
Figure 1-2: The Lagrange points of the Sun-Earth system.

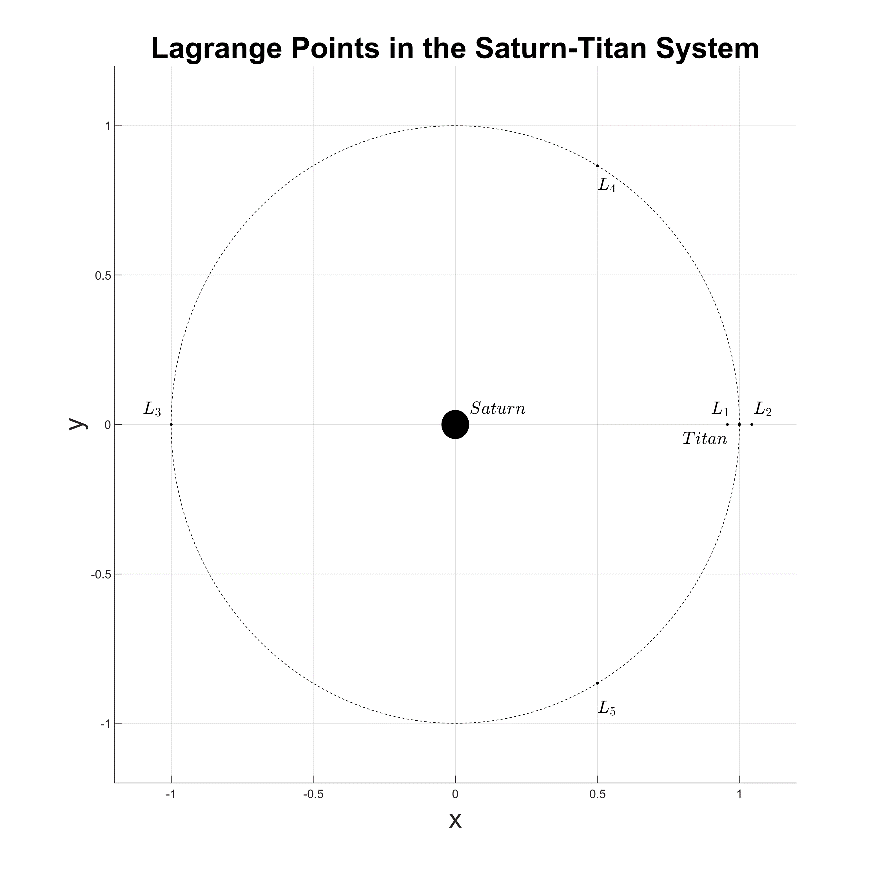
Figure 1-3: The Lagrange points of the Saturn-Titan system.